Rabu, 07 Oktober 2015
 Turunan Dalam Ruang Dimensi –n
Turunan Dalam Ruang Dimensi –n
05.47 | Diposting oleh
Rika Melyanti |
Edit Entri
TURUNAN DALAM RUANG DIMENSI –n
1.
Turunan Parsial
Turunan parsial fx (x,y) di (x0,y0)
dapat dijelaskan sebagai kemiringan dari garis singgung pada lengkung di (x0,y0)
atau turunan fungsi (x,y) terhadap variabel x. Jika pada perkuliahan Kalkulus
I, kita membahas turunan suatu fungsi yang menggunakan satu variabel, maka pada
Kalkulus lanjutan ini kita akan bahas turunan fungsi yang mengandung dua
variabel atau lebih.
Untuk menurunkan fungsi yang dimaksud, tidak dapat lagi menggunakan
cara biasa, melainkan kita harus turunkan sebagian-sebagian atau di partisi,
walaupun aturan baku turunan masih tetap dipakai.
Dalam matematika, turunan parsial sebuah fungsi matematika peubah banyak adalah turunannya terhadap salah satu peubah
(variabel) dengan peubah lainnya dipertahankan
(konstan). Ini dibedakan dengan turunan total,
yang membolehkan semua variabelnya untuk berubah. Turunan parsial berguna dalam
bidang kalkulus vektor dan geometri diferensial.
Turunan parsial sebuah fungsi f terhadap
variable x dituliskan oleh berbagai sumber rujukan sebagai:
Lambang turunan parsial ∂ adalah huruf bundar, diturunkan namun
berbeda dengan huruf Yunani
delta, dan dibedakan dengan notasi turunan total d (dan dari huruf ð).
Contoh 1
Jika Z = 8 + x2 – y2. Tentukan fy
(x,y) di titik x = 2 dan y = 5 !
Penyelesaian :
Dengan memberlakukan x sebagai konstan dalam fungsi Z = f(x,y) = 8 +
x2 – y2, maka kita dapat turunkan fungsi Z terhadap
variabel y, seperti berikut ;
fy (x,y) = -2y
fy (2,5) = -2 . 5 = -10
Contoh 2
Jika f (x,y) = x3y + 3y2. Tentukan fx
(2,3) dan fy (2,3) !
Penyelesaian :
fx (x,y) kita anggap y sebagai konstanta dan
mendiferensialkan fungsi f (x,y) terhadap x.
fx (x,y) = 3x2y + 0
fx (2,3) = 3 . 22 . 3
= 3 . 4 . 3 = 36
fx (x,y) kita anggap x sebagai konstantadan
mendiferensialkan fungsi f (x,y) terhadap y.
fy (x,y) = x3 +
6y
fy (2,3) = 23 + 6 . 3
= 8 + 18 = 26
Contoh 3
Penyelesaian :
fx (x,y) kita anggap y sebagai konstanta dan
mendiferensialkan fungsi f (x,y) terhadap x didapat ;
fx (x,y) = 2xy + 0
fx (1,2) = 2 . 1 . 2
= 4
= 4
Demikian
pula,
fy (x,y) = x2
+ 9y2
fy (1,2) = 12 + 9 . 22
= 1 + 36 = 37
Notasi-notasi lain yang digunakan dalam turunan parsial jika Z =
f(x,y) sebagai berikut :
2. Turunan Parsial Tingkat Tinggi
2. Turunan Parsial Tingkat Tinggi
Untuk fungsi turunan parsial dua variabel f(x,y) sebenarnya merupakan
fungsi lain dari dua peubah yang sama, turunan tersebut menurut Varberg dan
Purcell (Terjemahan Susila tahun 2010) dapat diturunkan secara parsial terhadap
x atau y untuk memperoleh empat buah turunan parsial kedua fungsi f, seperti
berikut :
|
|
Contoh 1
Tentukan semua turunan parsial tingkat dua fungsi f yang dirumuskan dengan
f(x, y) = 3x4y2 + xy2
+ 4y
Penyelesaian :
Turunan parsial tingkat tiga atau lebih tinggi didefinisikan dengan cara yang sama dan cara penulisannya pun serupa. Jadi jika f suatu fungsi dua peubah x dan y, turunan parsial ketiga f yang diperoleh dengan menurunkan f secara parsial.
Jika fungsi f(x, y) diturunkan secara
parsial terhadap x atau y maka kita akan memperoleh delapan buah turunan
parsial ketiga dari fungsi f,seperti berikut ini :
Kalau dilihat dari cara penulisan turunan parsial baik turunan tingkat dua
maupun tingkat tiga, ada perbedaan urutan penggunaan lambang ∂ dan f, yaitu
kalau pada penggunaan lambang ∂ pengerjaan penurunan dimulai dari urutan
variabel yang paling kanan, sedangkan pada penggunaan lambang f urutan
pengerjaan penurunan dimulai dari urutan variabel yang paling kiri atau yang
terdekat dengan f.
Seperti salah satu penurunan tingkat tiga dari fungsi f(x, y) berikut,
pertama kali terhadap x dan kemudian dua kali terhadap y, akan ditunjukan oleh
:
Perubahan lebih dari dua, misal f suatu fungsi tiga peubah x, y, dan z,
maka turunan parsial f terhadap x di (x, y, z)
Jadi, fx (x, y, z) boleh diperoleh dengan memperlakukan y dan z
sebagai konstanta dan menurunkan terhadap x.
Carilah turunan kedua fungsi f(x, y) = x2y3
+ x4y
Penyelesaian :
Langganan:
Posting Komentar (Atom)
About Me
Blog Archive
Followers
Diberdayakan oleh Blogger.
Copyright
Designed by Kaylah Kristine Designs | Powered by Blogger







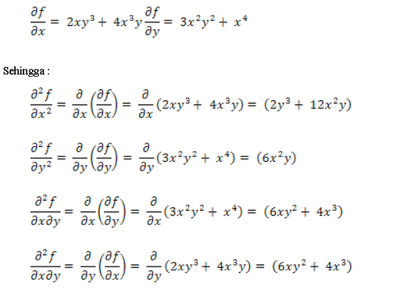


0 komentar:
Posting Komentar